2018-07-04

No.269 見栄っ張りの募金活動 | yukicoder

愚直なDPを考えてみる。

f(i, j, k) = 「i人目まで確定して、前の人がj円払った時、合計金額がk円である場合の数」

これでは間に合わない。

とりあえず、最初の人の募金額を0~Sの範囲で総当たりして固定し見てよう。先の人も含めて、少なくともその額を支払う必要がある。つまり、下図の斜線部は必ず支払われる。

f:id:parukii:20180704140039j:plain

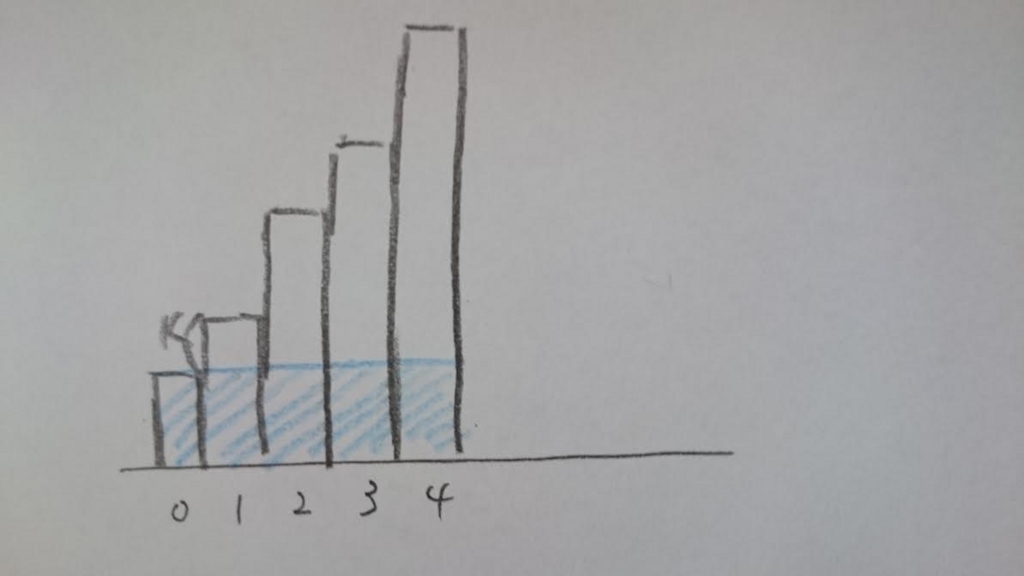
後の人々についても、その時点での支払確定の合計金額について注目することにする。先のDPの合計金額を、先の人も含む斜線部の支払い確定の金額に置き換えれば、前の人の支払った金額j円は情報として不要になる。というのは、この置き換えによって、（前の人の支払った金額+K）円以上ではなく、K円以上の範囲で支払い額を決めればよくなったため。

よって以下のようなDPを得る。

g(i, j) = 「i人目まで確定して、支払い確定の合計金額がj円である場合の数」

$g(i, j) = \sum_{k*(N-i) \leq j} g(i-1, j-k(N-i))$ で求まる。一見したところ全体でO(NS²)ほどの計算量がありそうだが、実際には最悪ケースで10⁹程度の計算量で済み、時間制限が5秒もあるので間に合う。

int N, S, K, M = (int)1e9+7;
cin >> N >> S >> K;
vi cu(S + 1), ne(S + 1);
int p = 0;
while (p*N <= S)cu[p++*N] = 1;
FOR(i, 1, N) {
    fill(all(ne), 0);
    rep(j, S + 1) {
        FOR(k, K, S + 1) {
            int l = j + k * (N - i);
            if (l > S)break;
            ne[l] += cu[j];
            if (ne[l] >= M)ne[l] -= M;
        }
    }
    swap(cu, ne);
}
cout << cu[S] << endl;

2018-07-03

AOJ1132 : Circle and Points

幾何

最適解が2点以上含む場合は、そのうちの2点を通る円でその最適解を必ず構成できる。

最適解を構成する頂点の集合をSとする。(|S|>=2)。Sの外側の点だけを拾って凸包を構成する。ただし、Sの点が一直線上に並ぶ場合は線分を構成する。これをTとおく。Sの点をすべて含むような円で、円周上には点が2個未満であるものを考えてみる。このとき、Tの隣接する2点以上に接してかつ、T上の点がすべて円の外側に出ないように円を動かすことができるはず。よって、この場合も最適解は|S|である。

そこで、与えられた頂点のうち2個を総当たりで選んで固定し、それらを通る円の中心を求め、そこからの距離が1以下の頂点を数えればいい。全体で計算量はθ(N³)となる。

2点A, Bを通る円の中心の求め方は以下の通り。A, Bの中点をMとする。また円の中心をCする。点Cから点Aへの距離は半径の1。線分AMの長さは、線分ABの長さの半分。よって、三角形AMCに三平方の定理を使ってCMの長さが求まる。ABの法線で長さが1であるものを $\vec{n}$ とおく。すると中心Cの座標は $\vec{OC} = \vec{OM} + CM\vec{n}$ より求まる。

2018-07-03

Marked Ancestor (AOJ 2170, JAG Summer 2009)

HL分解 Binary Indexed Tree

ライブラリがあれば楽にとけるやつ。HL分解して、マークしたかどうかはBinary Indexed Treeなどを使うだけ。

vector<vi> G(N);
FOR(i, 1, N) {
    int p;
    cin >> p;
    --p;
    G[p].push_back(i);
}

HLDecomposition hld(G);
// 0ならばマークされていない。
// そうでなければマークされている。
BIT bit(N);
bit.add(hld.id[0], 1);
// 解
ll re = 0;
rep(i, Q) {
    char c;
    int v;
    cin >> c >> v;
    --v;
    if (c == 'M') {
        // マークする
        bit.add(hld.id[v], 1);
    } else {
        // 根までの経路を半開区間の集合として得る
        auto H = hld.goUpToLCA(0, v);
        int p = 0;
        // 半開区間は頂点の深さの降順に並んでいる。
        // どの半開区間(経路の一部)に含まれるかを調べる
        // そのうち、深いもの
        for (; !bit.sum(H[p].first, H[p].second); p++);
        // この半開区間(経路の一部にふくまれている。)
        // 半開区間内では頂点は深さの昇順に並んでいる。
        // マークされている頂点を二分探索で求める。
        int ok = H[p].first, ng = H[p].second;
        while (ng - ok > 1) {
            int mid = (ok + ng) / 2;
            // 計算量はO(Nlog(N^2))
            (bit.sum(mid, H[p].second) ? ok : ng) = mid;
        }
        re += hld.ver[ok] + 1;
    }
}
cout << re << endl;

2018-07-02

E: Or Plus Max - AtCoder Regular Contest 100

集合

K番目の解をanswer(K)と表すことにする。

$f(x) = max_{i \lor j = x}(A_{i}+A_{j})$ とおくと $answer(K) = max_{1 \leq x \leq K}f(x)$ が解。

f(x)の条件の部分をもう少し緩くしてみる。

$g(x) = max_{i \lor j \subseteq x}(A_{i}+A_{j})$ とおくと、後者の(i, j)の集合は、前者のそれを含むので $f(x) \leq g(x)$ が成り立つ。更に、 $i \lor j \neq x かつ i \lor j \subseteq x$ のとき $i \lor j \lt x$ が成り立つ。したがって以下が成り立つ。

$answer(K) = max_{1 \leq x \leq K} g(x)$

g(x)が簡単に求まるとしてanswer(K)は $answer(K) \gets max(g(K), answer(K-1))$

g(x)の求め方を考えてみよう。和を最大にするには、 $i \subseteq x$ であるようなA[i]について大きい方から2個を選んで使えばいい。そのためには、単にxの部分集合を列挙しながら2値を更新していく。部分集合の列挙は計算量3^Nなので間に合う。ただし、定数倍が厳しいので注意。2値の更新を雑に書いたらTLEした。あと出力が多いのでprintfを使ってもいいかも。

auto upd = [](pii &a, int x) {
    if (x > a.second) {
        a.second = x;
        if (a.first < a.second)swap(a.first, a.second);
    }
};

int N;
cin >> N;
int M = 1 << N;
vi A(M);
rep(i, M) cin >> A[i];
int re = 0;
FOR(S, 1, M) {
    pii ma(0, 0);
    int T = S;
    do {
        upd(ma, A[T]);
        T = (T - 1)&S;
    } while (S != T);
    smax(re, ma.first + ma.second);
    cout << re << endl;
}

2018-07-02

D: Equal Cut - AtCoder Regular Contest 100

尺取法

BとCの間区切りを総当たりで固定する。

このとき、前半部分と後半部分の両方ともできるだけ均等に分けるのが最適。なぜか。

AとBの区切りを考えてみよう。AとBをできるだけ均等に（差が最小になるように）分けたときの小さい値をlow, 大きい値をhighとする。また、AとBをそれ以外の分け方にしたときの小さい値をLOW, 大きい値をHIGHとおく。A, Bの値同士の関係について言えば、均等に分けたほうがいいのはわかりやすい( $high - low \lt HIGH - LOW$ のため)。

分かりづらいのは、A, Bの値に対するC, Dの関係のほう。 $LOW \lt low \leq high \lt HIGH$ より、LOW, low, high, HIGHは以下の図のような座標を取るはず。 f:id:parukii:20180702142502j:plain どこにC, またはDの点をプロットしても、(A, B)の(C, D)に対する関係で言えば、最大値-最小値は(low, high)の組を使ったほうが小さいか等しいことがわかる。

CとDの区切りについても同様。

これで前半も後半もできるだけ均等に分けたほうがいいことがわかった。BとCの間の区切りを小さいほうから見ていくことを考えると、内側の区切りは前と同じかそれよりも右側にずれるかのいずれか。なので尺取り法が使える

2018-07-02

C: Linear Approximation - AtCoder Regular Contest 100

B[i] = A[i] - iとおく。入力例2ではB[i]は以下のような値をとっている。なお図ではb=2と仮置きしている。 f:id:parukii:20180702113347p:plain $\sum_{i=1}^{i=N}(A_{i}-(b+i)) = \sum_{i=1}^{i=N}(B_{i}-b)$ であるから、これは上図では点と直線y=bの距離の和を求めればいいことがわかる。直線bを上下に動かしてみると以下の事がわかる。

一番上の点よりも上に直線を持っていっても意味がない。
一番下の点よりも下に直線を持っていっても意味がない。
上の点が下の点よりも数が多い時、直線を上に持っていったほうがいい。
下の点が上の点よりも数が多い時、直線を下に持っていったほうがいい。
上の点と下の点の数が等しい時、直線を上下しても結果は変わらない。

よってbの値はBだけ調べればいいことがわかる。

とりあえず、bを一番低い値に設定して解候補を計算してみる。あとは、bを上へずらしていって、差分と上下の点の数を使って、解候補を加減すればいい。

int N;
cin >> N;
vi A(N), B(N), C;
rep(i, N) {
    cin >> A[i];
    B[i] = A[i] - (i + 1);
}
sort(all(B));
C = B;
C.erase(unique(all(C)), C.end());

ll sm = 0;
rep(i, N)sm += B[i] - C[0];
ll re = sm;

ll p = 0;
FOR(i, 1, sz(C)) {
    while (p < N && B[p] < C[i])++p;
    ll q = N - p;
    sm += (p - q) * (C[i] - C[i - 1]);
    smin(re, sm);
}

cout << re << endl;

2018-06-30

AOJ 2333 : 僕の友達は小さい My friends are small (JAG Summer 2010)

DP 数え上げ

まずは簡単な例外的な組合せから数えてみる。以下、解をanswerと表記する。どの友達もリュックに入れることができないならばanswer+=1。また、すべての友達をリュックに入れることができるならばanswer+=1。

それ以外の場合を数える。とりあえずリュックに入れない友達の最小の重さmを総当たりにより固定する。これはたかだかN通り。このとき重さm未満の友達はすべてリュックに入るはずだから、少なくとも $\sum_{w\lt m}w$ の重さの友達をリュックに入れる。さて、注意しなければいけないのは、重さmの友達が１人とは限らないことである。重さmの友達の人数を $g(m)$ と表記することにする。重さmの友達を $x\lt g(m)$ 人選ぶ方法は $\binom{g(m)}{x}$ 通りである。このとき重さの和は、重さm未満の友達も考慮に入れると $\sum_{w\lt m}w + xm$ である。

mごとにDPを解く。

dp(i, j) := 「重さi-1の友達の状態まで確定した時、リュックに入った友達の重さの和がjである。そのような場合の数」

とする。これを先の $\sum_{w\lt m}w + xm$ によってDPを初期化してから計算していく。重さmの友達が入れられない状態のみを計算するので $answer += \sum_{m>W-j}dp(最後の友達まで確定, j)$ とする。

計算量は全体でO(WN²)

vector<vector<int>> combinations(int n, int mod) {
    auto res = vector<vector<int>>(n + 1, vector<int>(n + 1));
    rep(i, n + 1) res[i][0] = 1;
    for (int i = 1; i <= n; ++i) for (int j = 1; j <= i; ++j)
        res[i][j] = (res[i - 1][j - 1] + res[i - 1][j]) % mod;
    return res;
}

int N, W, wt[201], M;
vector<vi> C;
vector<pii> we;
mint dp[201][10001];

mint f(int s) {
    int mi = we[s].first;
    FOR(i, s + 1, M) {
        int w, num;
        tie(w, num) = we[i];
        rep(j, num + 1) {
            rep(k, W + 1) {
                if (j*w + k <= W) {
                    dp[i + 1][j*w + k] += dp[i][k] * C[num][j];
                }
            }
        }
    }
    mint re;
    FOR(i, 1, W + 1) {
        if (mi > W - i)re += dp[M][i];
    }
    return re;
}

int main() {
    C = combinations(200, 1000000007);

    cin >> N >> W;
    rep(i, N) {
        cin >> wt[i];
    }
    sort(wt, wt + N);

    int pre = -1;
    rep(i, N) {
        if (wt[i] != pre) {
            we.push_back(mp(wt[i], 0));
        }
        we.back().second++;
        pre = wt[i];
    }

    mint re;
    M = sz(we);
    int sm = 0;
    rep(i, M) {
        MEM(dp, 0);
        int num = we[i].second;
        rep(j, num) {
            if (sm <= W) {
                dp[i + 1][sm] += C[num][j];
            }
            sm += we[i].first;
        }
        re += f(i);
    }
    if (sm <= W)re += 1;
    if (wt[0] > W)re += 1;
    cout << re << endl;
}