No.269 見栄っ張りの募金活動 | yukicoder

愚直なDPを考えてみる。

f(i, j, k) = 「i人目まで確定して、前の人がj円払った時、合計金額がk円である場合の数」

これでは間に合わない。

とりあえず、最初の人の募金額を0~Sの範囲で総当たりして固定し見てよう。先の人も含めて、少なくともその額を支払う必要がある。つまり、下図の斜線部は必ず支払われる。

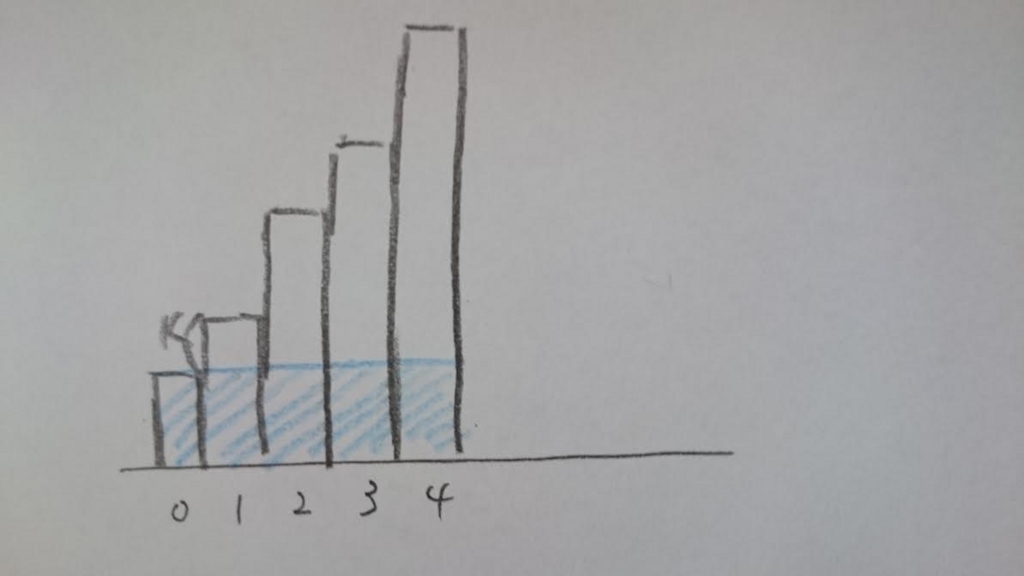
後の人々についても、その時点での支払確定の合計金額について注目することにする。先のDPの合計金額を、先の人も含む斜線部の支払い確定の金額に置き換えれば、前の人の支払った金額j円は情報として不要になる。というのは、この置き換えによって、（前の人の支払った金額+K）円以上ではなく、K円以上の範囲で支払い額を決めればよくなったため。

よって以下のようなDPを得る。

g(i, j) = 「i人目まで確定して、支払い確定の合計金額がj円である場合の数」

で求まる。一見したところ全体でO(NS²)ほどの計算量がありそうだが、実際には最悪ケースで10⁹程度の計算量で済み、時間制限が5秒もあるので間に合う。

int N, S, K, M = (int)1e9+7;
cin >> N >> S >> K;
vi cu(S + 1), ne(S + 1);
int p = 0;
while (p*N <= S)cu[p++*N] = 1;
FOR(i, 1, N) {
    fill(all(ne), 0);
    rep(j, S + 1) {
        FOR(k, K, S + 1) {
            int l = j + k * (N - i);
            if (l > S)break;
            ne[l] += cu[j];
            if (ne[l] >= M)ne[l] -= M;
        }
    }
    swap(cu, ne);
}
cout << cu[S] << endl;