2018-07-02

D: Equal Cut - AtCoder Regular Contest 100

尺取法

BとCの間区切りを総当たりで固定する。

このとき、前半部分と後半部分の両方ともできるだけ均等に分けるのが最適。なぜか。

AとBの区切りを考えてみよう。AとBをできるだけ均等に（差が最小になるように）分けたときの小さい値をlow, 大きい値をhighとする。また、AとBをそれ以外の分け方にしたときの小さい値をLOW, 大きい値をHIGHとおく。A, Bの値同士の関係について言えば、均等に分けたほうがいいのはわかりやすい( $high - low \lt HIGH - LOW$ のため)。

分かりづらいのは、A, Bの値に対するC, Dの関係のほう。 $LOW \lt low \leq high \lt HIGH$ より、LOW, low, high, HIGHは以下の図のような座標を取るはず。 f:id:parukii:20180702142502j:plain どこにC, またはDの点をプロットしても、(A, B)の(C, D)に対する関係で言えば、最大値-最小値は(low, high)の組を使ったほうが小さいか等しいことがわかる。

CとDの区切りについても同様。

これで前半も後半もできるだけ均等に分けたほうがいいことがわかった。BとCの間の区切りを小さいほうから見ていくことを考えると、内側の区切りは前と同じかそれよりも右側にずれるかのいずれか。なので尺取り法が使える

2018-07-02

C: Linear Approximation - AtCoder Regular Contest 100

B[i] = A[i] - iとおく。入力例2ではB[i]は以下のような値をとっている。なお図ではb=2と仮置きしている。 f:id:parukii:20180702113347p:plain $\sum_{i=1}^{i=N}(A_{i}-(b+i)) = \sum_{i=1}^{i=N}(B_{i}-b)$ であるから、これは上図では点と直線y=bの距離の和を求めればいいことがわかる。直線bを上下に動かしてみると以下の事がわかる。

一番上の点よりも上に直線を持っていっても意味がない。
一番下の点よりも下に直線を持っていっても意味がない。
上の点が下の点よりも数が多い時、直線を上に持っていったほうがいい。
下の点が上の点よりも数が多い時、直線を下に持っていったほうがいい。
上の点と下の点の数が等しい時、直線を上下しても結果は変わらない。

よってbの値はBだけ調べればいいことがわかる。

とりあえず、bを一番低い値に設定して解候補を計算してみる。あとは、bを上へずらしていって、差分と上下の点の数を使って、解候補を加減すればいい。

int N;
cin >> N;
vi A(N), B(N), C;
rep(i, N) {
    cin >> A[i];
    B[i] = A[i] - (i + 1);
}
sort(all(B));
C = B;
C.erase(unique(all(C)), C.end());

ll sm = 0;
rep(i, N)sm += B[i] - C[0];
ll re = sm;

ll p = 0;
FOR(i, 1, sz(C)) {
    while (p < N && B[p] < C[i])++p;
    ll q = N - p;
    sm += (p - q) * (C[i] - C[i - 1]);
    smin(re, sm);
}

cout << re << endl;

2018-06-30

AOJ 2333 : 僕の友達は小さい My friends are small (JAG Summer 2010)

DP 数え上げ

まずは簡単な例外的な組合せから数えてみる。以下、解をanswerと表記する。どの友達もリュックに入れることができないならばanswer+=1。また、すべての友達をリュックに入れることができるならばanswer+=1。

それ以外の場合を数える。とりあえずリュックに入れない友達の最小の重さmを総当たりにより固定する。これはたかだかN通り。このとき重さm未満の友達はすべてリュックに入るはずだから、少なくとも $\sum_{w\lt m}w$ の重さの友達をリュックに入れる。さて、注意しなければいけないのは、重さmの友達が１人とは限らないことである。重さmの友達の人数を $g(m)$ と表記することにする。重さmの友達を $x\lt g(m)$ 人選ぶ方法は $\binom{g(m)}{x}$ 通りである。このとき重さの和は、重さm未満の友達も考慮に入れると $\sum_{w\lt m}w + xm$ である。

mごとにDPを解く。

dp(i, j) := 「重さi-1の友達の状態まで確定した時、リュックに入った友達の重さの和がjである。そのような場合の数」

とする。これを先の $\sum_{w\lt m}w + xm$ によってDPを初期化してから計算していく。重さmの友達が入れられない状態のみを計算するので $answer += \sum_{m>W-j}dp(最後の友達まで確定, j)$ とする。

計算量は全体でO(WN²)

vector<vector<int>> combinations(int n, int mod) {
    auto res = vector<vector<int>>(n + 1, vector<int>(n + 1));
    rep(i, n + 1) res[i][0] = 1;
    for (int i = 1; i <= n; ++i) for (int j = 1; j <= i; ++j)
        res[i][j] = (res[i - 1][j - 1] + res[i - 1][j]) % mod;
    return res;
}

int N, W, wt[201], M;
vector<vi> C;
vector<pii> we;
mint dp[201][10001];

mint f(int s) {
    int mi = we[s].first;
    FOR(i, s + 1, M) {
        int w, num;
        tie(w, num) = we[i];
        rep(j, num + 1) {
            rep(k, W + 1) {
                if (j*w + k <= W) {
                    dp[i + 1][j*w + k] += dp[i][k] * C[num][j];
                }
            }
        }
    }
    mint re;
    FOR(i, 1, W + 1) {
        if (mi > W - i)re += dp[M][i];
    }
    return re;
}

int main() {
    C = combinations(200, 1000000007);

    cin >> N >> W;
    rep(i, N) {
        cin >> wt[i];
    }
    sort(wt, wt + N);

    int pre = -1;
    rep(i, N) {
        if (wt[i] != pre) {
            we.push_back(mp(wt[i], 0));
        }
        we.back().second++;
        pre = wt[i];
    }

    mint re;
    M = sz(we);
    int sm = 0;
    rep(i, M) {
        MEM(dp, 0);
        int num = we[i].second;
        rep(j, num) {
            if (sm <= W) {
                dp[i + 1][sm] += C[num][j];
            }
            sm += we[i].first;
        }
        re += f(i);
    }
    if (sm <= W)re += 1;
    if (wt[0] > W)re += 1;
    cout << re << endl;
}

2018-06-29

１０歳の動的計画 (AOJ 2335) (JAG Summer 2010)

カタラン数

とりあえず縦横を別々に考えられる。よって、縦でx回寄り道して座標Nにいる場合の数をf(x), 横でy回寄り道して座標Mにいる場合の数をg(y)とすると $\sum_{x+y=K} f(x)g(y) \binom{N+M+2K}{N+2x}$ が解である。ここで $\binom{N+M+2K}{N+2x}$ は縦の移動と横の移動を別々にみたあとにマージするとして、そのマージの仕方の数。N+M+2K回の移動のうち、どのN+2x回の移動を縦の移動に割り当てるかを表す。

問題はf(x), g(y)の求め方になる。

寄り道回数 $0\leq x \leq K$ について縦方向の移動で「負の座標を認めて」座標Nまで行く場合の数をF(x)とおくと $F(x) = \binom{N+2x}{x}$ である。

ここから「負の座標になってしまった」場合の数を取り除いていく。ちょうど $z+1 \leq x$ 回目の寄り道で「初めて」負の座標-1に到達してしまう時を考えてみよう。このとき、直前のちょうどz回目の寄り道によって座標0にいるはずである。前進z回、寄り道z回で「負の座標にならずに」座標0にいる場合の数は、いわゆるカタラン数と呼ばれるもので $C(z)$ と表すことにする。

「負の座標を認めず座標0」＝＞「一歩後退して座標-1」＝＞「負の座標を認めて座標Nまで移動」

あとは最後の部分を計算する。ちょうどz+1回寄り道したので残りの寄り道回数はx-z-1回。合計N+x-z-1回の移動のうち、x-z-1回寄り道して「負の座標を認めて」座標Nに到達する場合の数は $\binom{N+2(x-z-1)}{x-z-1}$ である。

以上により $f(x) = \binom{N+2x}{x} - \sum_{0\leq z \lt x}{C(z)\binom{N+2(x-z-1)}{x-z-1}}$ となる。 g(y)も同様に求まる。

namespace comb {
    const int N = 300001;
    mint fact[N];
    mint rev[N];
 
    void init() {
        fact[0] = 1;
        for (int i = 1; i < N; ++i)fact[i] = fact[i - 1] * i;
        for (int i = 0; i < N; ++i)rev[i] = fact[i].inverse();
    }
 
    mint C(int n, int r) {
        if (n < r)return 0;
        return fact[n] * rev[r] * rev[n - r];
    }

    mint catalan(int n) {
        return fact[2 * n] * rev[n + 1] * rev[n];
    }
}
 
int N, M, K;
 
vector<mint> f(int n) {
    vector<mint> res(K + 1);
    rep(i, K + 1) {
        mint x = comb::C(n + 2 * i, i);
        rep(j, i) {
            int k = i - j - 1;
            x -= comb::catalan(j) * comb::C(n + 1 + 2 * k, k);
        }
        res[i] = x;
    }
    RT res;
}
 
int main() {
    comb::init();
 
    cin >> N >> M >> K;
 
    mint ans;
    auto A = f(N);
    auto B = f(M);
    rep(i, K + 1) {
        int j = K - i;
        ans += A[i] * B[j] * comb::C(N + M + K * 2, N + i * 2);
    }
    cout << ans << endl;
}

2018-06-24

D - Snuke Numbers | AtCoder Regular Contest 099

証明なしで思いつき方だけ書いておく。自然数nがすぬけ数あるためには $n/S(n)\leq m/S(m)$ がnより大きいすべてのmについて成り立たなければならない。まず、十分大きいmに対して、S(n), S(m)の値は十分小さいので $n/S(n) \leq m/S(m)$ と見做してよい。小さめの自然数nについて、十分大きなm(ここでは10⁷まで確かめる)まで不等式をチェックすることで、適当に小さい方から順にすぬけ数っぽいものを出力してみる。

これは以下のコードにより得た。

ll s(ll x) {
    ll re = 0;
    while (x > 0) {
        re += x % 10;
        x /= 10;
    }
    RT re;
}

bool cmp(ll x, ll y) {
    RT x*s(y) <= y * s(x);
}

void test(int K) {
    for (int n = 1; n <= 100001 &&K > 0; ++n) {
        bool ok = true;
        for (int m = n + 1; m <= 10000000; ++m) {
            if (!cmp(n, m)) {
                ok = false;
                break;
            }
        }
        if (ok) {
            K--;
            cout << n << endl;
        }
    }
}

ある数列の性質を知りたい時、隣接する項を調べることはよくある。二項の差をとってみると以下を得る。

規則が見つかった。

void solve(int K) {
    ll d = 1, cur = 0;
    rep(i, K) {
        ll x = cur + d, y = cur + d * 10;
        if (cmp(x, y)) {
            cur = x;
        } else {
            cur = y;
            d *= 10;
        }
        cout << cur << endl;
    }
}

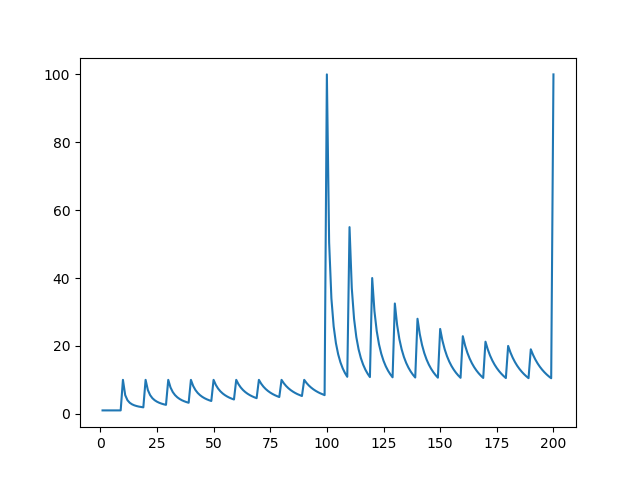
ちなみにn/S(n)の値の増減は以下の図のようになっている。 f:id:parukii:20180624212859p:plain f:id:parukii:20180624213109p:plain

2018-05-30

A. Fair | Codeforces Round #485 (Div. 1)

BFS

各商品をスタート地点として見てBFSっぽいことをする。はじめにキューへすべての始点入れておくだけ。

int N, M, K, S;

vi G[100005];
int dis[100005][102];
vi pos[102];

void bfs(int kind) {
    queue<pii> Q;
    each(p, pos[kind]) {
        Q.push({ p,0 });
        dis[p][kind] = 0;
    }
    while (sz(Q)) {
        int u, d;
        tie(u, d) = Q.front();
        Q.pop();
        each(v, G[u]) {
            if (dis[v][kind] == -1) {
                dis[v][kind] = d + 1;
                Q.push({ v, d + 1 });
            }
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout << fixed << setprecision(20);

    MEM(dis, -1);
    cin >> N >> M >> K >> S;
    rep(a, N) {
        int kind;
        cin >> kind;
        pos[--kind].push_back(a);
    }
    rep(a, M) {
        int u, v;
        cin >> u >> v;
        --u; --v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    rep(a, K) {
        bfs(a);
    }
    rep(a, N) {
        sort(dis[a], dis[a] + K);
        int re = accumulate(dis[a], dis[a] + S, 0);
        cout << re << ' ';
    }
    cout << endl;
}

2018-05-30

B. Petr and Permutations | Codeforces Round #485 (Div. 1)

Binary Indexed Tree

転倒数の偶奇は操作回数のそれと等しい。

$l, r \in \mathbb{N}, 1 \leq l \lt r \leq N$ とおく。 l番目の要素とr番目の要素を交換したとする。 l番目とr番目の間にz個の要素があるとする。
また、そのうち、もとのl番目より大きい要素をgL個, 小さい要素をlL(=z-gL)個とする。まずl番目と間z個の関係だけで転倒数の増減を見ると
gL - lL = gL - (z-gL) = 2gL-z
だけ転倒数が増減する。
同様にr番目より大きい要素をgR個, 小さい要素をlR(=z-gR)個とすると、r番目と間の要素で
lR - gR = (z-gR)-gR = z-2gR
だけ増減する。更に、l番目とr番目の関係だけ見ると転倒数が+-1だけ増減するので全体で
(2gL-z)+(z-2gR)+-1=2(gL-gR)+-1
だけ転倒数が増減することがわかる。よって、1回の操作での転倒数の増減は常に奇数

long long inversionNumber(const vector<int> &a) {
    long long res = 0;
    int n = (int)a.size();
    BinaryIndexedTree<long long> bit(n + 1);
    for (int x : a) {
        res += bit.sum(x + 1, n + 1);
        bit.add(x, 1);
    }
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout << fixed << setprecision(20);

    int N;
    cin >> N;
    vi A(N);
    each(a, A)cin >> a, --a;
    ll inv = inversionNumber(A);
    string re = "Um_nik";
    if (3 * N % 2 == inv % 2)re = "Petr";
    cout << re << endl;
}