D - Snuke Numbers | AtCoder Regular Contest 099

証明なしで思いつき方だけ書いておく。 自然数nがすぬけ数あるためには がnより大きいすべてのmについて成り立たなければならない。 まず、十分大きいmに対して、S(n), S(m)の値は十分小さいので と見做してよい。 小さめの自然数nについて、十分大きなm(ここでは10⁷まで確かめる)まで不等式をチェックすることで、適当に小さい方から順にすぬけ数っぽいものを出力してみる。

1
2
3
4
5
6
7
8
9
19
29
39
49
59
69
79
89
99
199
299
399
499
599
699
799
899
999
1099
1199
1299
1399
1499
1599
1699
1799
1899
1999
2999
3999
4999
5999
6999
7999
8999
9999
10999
11999
12999
13999
14999
15999
16999
17999
18999
19999
...

これは以下のコードにより得た。

ll s(ll x) {
    ll re = 0;
    while (x > 0) {
        re += x % 10;
        x /= 10;
    }
    RT re;
}

bool cmp(ll x, ll y) {
    RT x*s(y) <= y * s(x);
}

void test(int K) {
    for (int n = 1; n <= 100001 &&K > 0; ++n) {
        bool ok = true;
        for (int m = n + 1; m <= 10000000; ++m) {
            if (!cmp(n, m)) {
                ok = false;
                break;
            }
        }
        if (ok) {
            K--;
            cout << n << endl;
        }
    }
}

ある数列の性質を知りたい時、隣接する項を調べることはよくある。二項の差をとってみると以下を得る。

1
1
1
1
1
1
1
1
10
10
10
10
10
10
10
10
10
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
1000
10000
10000
10000
...

規則が見つかった。

void solve(int K) {
    ll d = 1, cur = 0;
    rep(i, K) {
        ll x = cur + d, y = cur + d * 10;
        if (cmp(x, y)) {
            cur = x;
        } else {
            cur = y;
            d *= 10;
        }
        cout << cur << endl;
    }
}

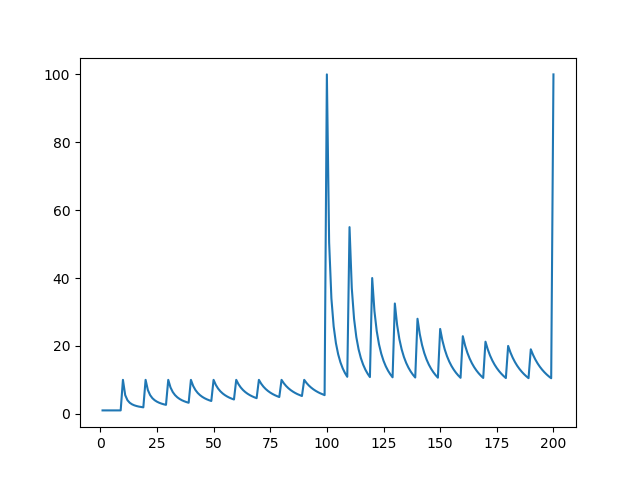
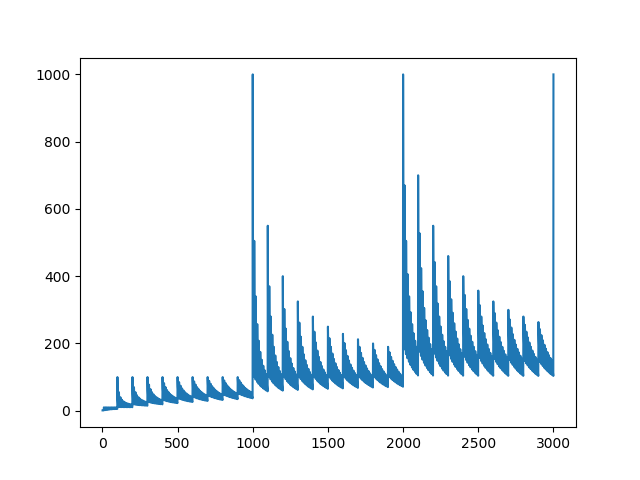
ちなみにn/S(n)の値の増減は以下の図のようになっている。