yukicoder #483: マッチ並べ

各座標を頂点としてグラフを書く。連結成分ごとに考えてみる。

グラフが木になる場合は、根付き木と見なして親から子へ、マッチの頭薬を向けて並べていけばいい。

グラフが閉路を1個だけもつ場合。まず、その1個の閉路を、片方向（時計回り、反時計回りどちらでも)にならべていく。そうしたら、先の方法と同様に、サイクルを根付き木の根と見なして残りのマッチを並べていけばいい。

グラフが閉路を2個以上もつ場合はこれらの埋め方は不可。

 

閉路が2個以上あるかどうかの判定は次数の合計を見ればいい。

次数/2 = 頂点数-1

のときは木

次数/2 = 頂点数

のときは閉路1個

次数/2 > 頂点数

のときは閉路2個以上

f:id:parukii:20170213134222j:plain

yukicoder #250: atetubouのzetubou

実行時間をf(X,D)とすると

f(X,D) = (X+D-1)!/(X!(D-1)!)

これを普通に計算するとオーバーフローなどが面倒。

なのでとりあえず素因数分解した形で、肩の足し引きだけしておく。

素因数を１個ずつ掛けていって、tを超えないか、オーバーフローしないかをチェックする。

SRM 638 DIV1 Medium: NarrowPassage2

解法は簡単だが思いつけないタイプ

解法

分割統治法、再帰

 

maxSizeSum=10で色々やってみる。

m = min(size), M = max(size)

とする。

size = {5,2,3,4,6}

のような場合

m = 2, M = 6

であり、

m+M <= maxSizeSumが成り立つので

2はどこにでもおける。

すなわち、2の各位置について、他の要素の並べ方は別々に考えることができる。

つまり

size' = {5,3,4,6}

 の並べ方1通りに対して、2を好きな箇所に挿入でき、挿入できる位置は|size|通り。

これで部分問題

count(size', maxSizeSum)

が得られた。

今度はm+M > maxSizeSum のときを考える。

size = {3,2,5,9,4,6}

とすると

m = 2, M = 9

であり m + M = 11 > maxSizeSum

Mに隣接する値は常にm以上であるはずだから、Mを隣接する値と交換することはできない。つまり、Mの位置は固定された。また、Mより左にある要素はMより右へは行けない。同様にMより右にある要素はMより左へはいけない。なので数列から値がMである要素を一つ取り除いて

left = {3,2,5}, right = {4, 6}

 のようにMの左右の列は別々に並び替えることができる。

よって

部分問題

count(size, maxSizeSum) = count(left, maxSizeSum) * count(right, maxSizeSum)

であり、

もとの問題は部分問題

count(left,maxSizeSum)とcount(right, maxSizeSum)に分割することができた。

最後に再帰の底を考えると、|size|<=1で並べ方は1通りしかない。

思いつきたかった

最小値や最大値が特異な動きをするのは簡単に思いつけそう。少し手を動かして実験をしてみれば、最小値が自由に動ける場合や最大値が固定される場合に気づく？もし最大値が固定される場合に気づけば、その場合は部分問題に分割できることは明らか。そうでない場合を考えてみる。こちらも部分問題に分割できる。分割統治法。あとは再帰の形で表せればいい。

SRM 708 DIV2 Hard: PalindromicSubseq2

dp[i][j]:=左は文字iまで、右側はjまで見たときの偶数長(長さ0以上)の回分の個数の数(ただし1<=i<=j<=N)

たとえば、文字列sが以下のような形の場合(1-indexed)

abcxycba

abc...ba

dp[3][7] = 2^2 = 4

1<=j-i<=nを

nから順に確定していけばいい。つまり

dp[i][j]

= dp[i-1][j] + dp[i][j+1] - dp[i-1][j+1] + (s[i]==s[j]?dp[i-1][j+1]:0)

= dp[i-1][j] + dp[i][j+1] - (s[i]==s[j]?0:dp[i-1][j+1])

f:id:parukii:20170210135639j:plain

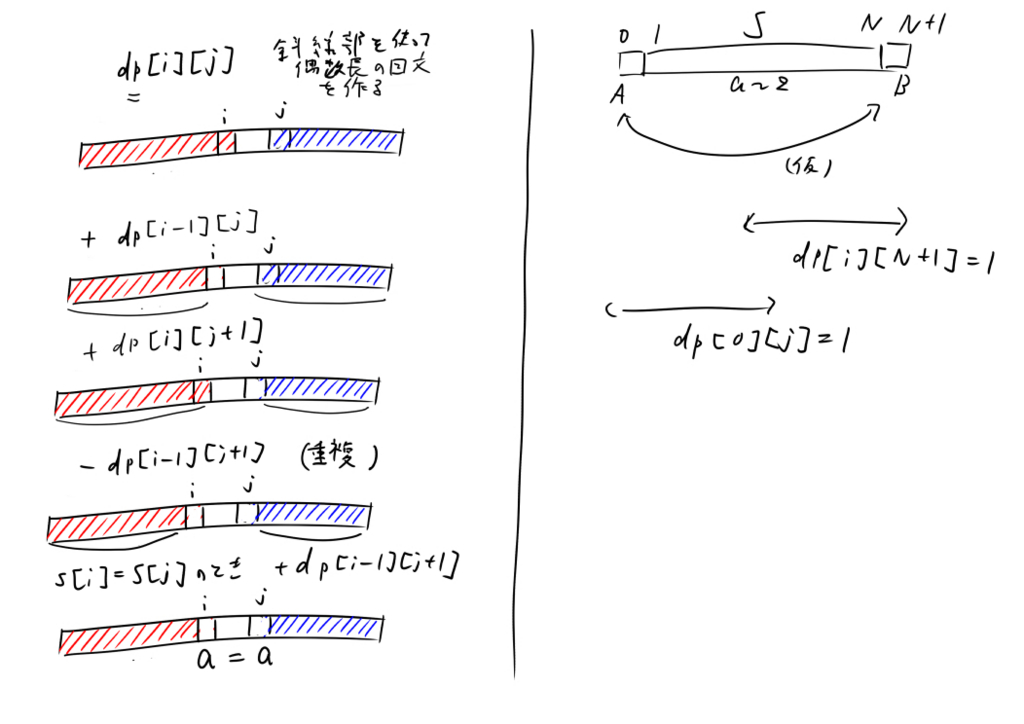
SRM 708 DIV1 Easy: BalancedStrings

文字列s[0]~s[N-1]の文字列の末尾に文字追加して解を構成すことを考える。
ある文字列s[i]に文字を追加したときに全体で、instabilityは0~1、similarityは0~100*(N-1)増加する。
このようにinstabilityの値のほうが調整がし易い。
そこでまずsimilarityが小さくなるようにざっくりs[0]~s[N-1]を作ってinstabilityをインクリメントしていく。
similarityを小さくするにはできるだけs[0]~s[N-1]が文字を共有しないでほしいので以下のような簡単な構成が思いつく。
すなわち
s[i] = 'a' + (i mod 26)
この種の構成法について
N=100 の一番面倒な場合についてだけ考えてみる。
i番目の文字列についてj<iでかつs[i] = s[j]であるものはj/26 個ある。
これでsimilarityは数えられた。|s[i]| = 1 よりinstability=0。
similarityに追いつくようinstabilityを増やしていけばよいのだが、similarityの増加の仕方が厄介そうなのは明らか。
similarityが定まったら、similarityを増加させないでinstabilityを調整できれば楽なのだが、そのような構成法はあるだろうか。
ある。実は今まで使っていない文字が2種類以上あるならば、単にその2文字(仮にA,Bとすると)
s[0] + A + B + A + B ... (100文字まで)
のようにAとBを末尾に追加すればよい。
同様に未使用の文字CとDがあるとして
s[1] + C + D + C + D ....(100文字まで)
未使用の文字が必要だったので
s[i]の構成を
s[i] = 'a' + (i mod M) (M<26)に変更しよう。
N=100のときにinstabilityが最大になるのは明らかで、未使用の文字の種類が最大になる。
このときM=22とすると都合がいい。すなわちw,x,y,zの4文字でinstabilityを調整する。
最終的に解は
s[0] = awxwxwxwx...
s[1] = byzyzyzyz...
s[2] = c
s[3] = d
...
のような形になる。