Educational Codeforces Round 21 D: Array Division
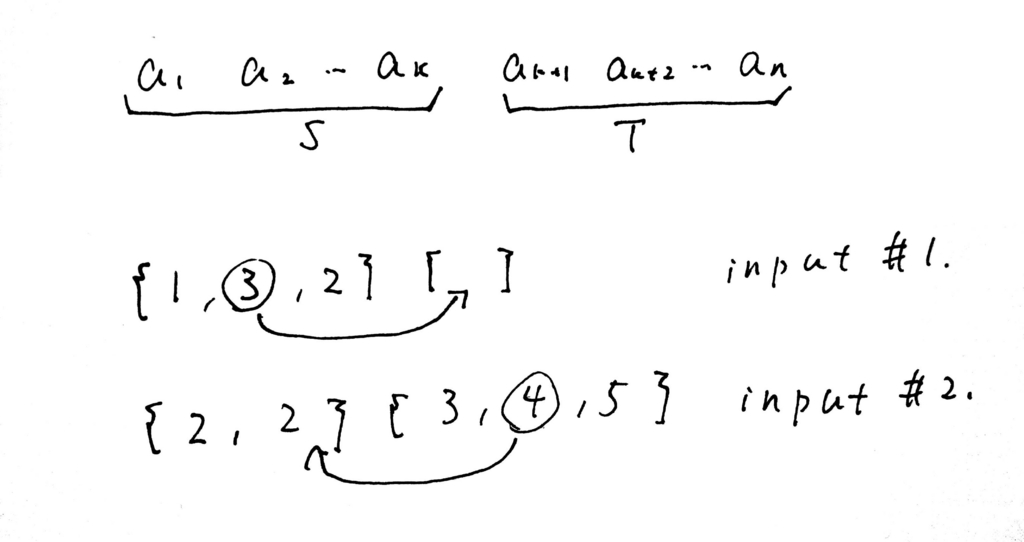
n=1のとき明らかにNO
よってn>=2とする。
とりあえず、挿入は考えずに配列を前の部分(S)と後の部分(T)に分けてみる。ただし、S,Tは空であってもよいとする。
z=Σ[x∈S](x), w=Σ[y∈T](y)とする。
場合1. z=wの場合
ある要素を選んで同じ場所に挿入すればいいからYES
場合2. z>wの場合
Sから値vを取り除いてTに挿入したときに和が等しくなればYES
すなわち
z-v = w+vより
v = (z-w)/2としてv∈SならばYES
場合3. w>zの場合
場合2.と同様
S,Tはすべて試す。つまり、全ての前の部分の長さ(後ろの部分の長さ)を総当りで固定して、上記のチェックをすればいい。
Educational Codeforces Round 21 E: Selling Souvenirs
エディトリアル見て書いたコード。コメントつき
/* エディトリアルのとおりの解法 */ /* 重さ1, 2のsouvenirだけを使ったとき、重さの和がiとする。 このときdp[i]=(x,y,z)は以下の意味。 xはコストの和の最大値 yは重さ1のsouvenirをいくつ使ったか。 zは重さ2のsouvenirをいくつ使ったか。 インデックスのほうにy,zのような情報を持たせないで、最適値の後ろにくっつけてる。 */ tuple<ll, int, int> dp[300001]; int main(){ ios::sync_with_stdio(false); cin.tie(0); int N, M; cin >> N >> M; vll weight(N), cost(N); rep(i, N) { cin >> weight[i] >> cost[i]; } // 重さの種類は3種類しかないのでバケツソートしておく。 vll costByWeight[4]; rep(i, N)costByWeight[weight[i]].push_back(cost[i]); // とりあえず、コストの大きい方から使いたいのでソートしておく。 rep(i, 4)sort(costByWeight[i].rbegin(), costByWeight[i].rend()); FOR(i, 1, M + 1)dp[i] = mt(-1ll, -1, -1); rep(i, M) { ll sumCost; int cnt1, cnt2; tie(sumCost, cnt1, cnt2) = dp[i]; if (sumCost == -1)continue; if (cnt1 < sz(costByWeight[1])) { smax(dp[i + 1], mt(sumCost + costByWeight[1][cnt1], cnt1 + 1, cnt2)); } if (cnt2 < sz(costByWeight[2]) && i + 2 <= M) { smax(dp[i + 2], mt(sumCost + costByWeight[2][cnt2], cnt1, cnt2 + 1)); } } /* maxCost[i]は1,2の重さのsouvenirだけ使ったとき、重さの和がi以下である場合のコストの最大値 */ vector<ll> maxCost(M + 1); rep(i, M) { maxCost[i + 1] = max(maxCost[i], get<0>(dp[i + 1])); } // sumThreeは重さ3のsouvenirのコストの和 ll answer = 0, sumThree = 0; // 重さ3のsouvenirのコストを総当りで固定する for (int i = 0; i <= M && i / 3 <= sz(costByWeight[3]); i += 3) { // 事前に計算したDPをうまく使って、解を更新する smax(answer, sumThree + maxCost[M - i]); if (i / 3 < sz(costByWeight[3])) { sumThree += costByWeight[3][i / 3]; } } cout << answer << endl; }
Educational Codeforces #21 G: Anthem of Berland

上図は3番目の入力例の文字列t="abcab"にダミーの1文字を加えたt+'#'="abcab#"に対してKMP法のDFAを描いたもの。!はその他の文字を表す。
tはオーバーラップしてもよいので、最終状態からの遷移もほしい。そこで、末尾にダミーの文字を加えた。これにより、最終状態からの遷移も得られた。
例えば
abcabと最後まで一致した後、
cが来た場合
接頭辞abcと一致するはず。実際、上図でそのような遷移が得られる。
|s|*|t|<=10^7という特殊な制約に注意しよう。
これにより、KMP法の計算以外ではO(|s|*|t|)の実行時間が許されている。
dp[i][j]を「Sの文字列をi番目まで確定していてDFA上で状態がjであるときの、DFA上のダミーでない最終状態に到達した回数の最大値」
とすれば、max(dp[|s|][j])が解。
Codeforces #413 E: Aquarium decoration
解説付きコード
/* 解説 二人とも好むアイテムの集合をX, MashaだけのはY, ArkadyだけのはZとする 全体でちょうどm個でなければならないが、とりあえずそのことは考えない。 Xからx個選ぶとする。xは|X|から0まで総当りする。 k-x個だけYとZから取る必要があるので取る。 ただし、YまたはZからk-x個取れない場合があるが、このとき条件を満たさない。 YとZから取った個数をy, zとする。ただし、y=z 明らかに x+y+z<=m である必要がある。 逆にこの時、残ったアイテムからm-(x+y+z)個を安い方から貪欲に取ればいい。 m-(x+y+z)個のアイテムの値段の和を得るために Binary Indexed Treeを使う。 BIT を2個もちそれぞれcnt, sumとする。 アイテムが価格順であるとき、 cnt: クエリ[l, r)に対して[l, r)のうち残っているのはいくつあるか sum: クエリ[l, r)に対して[l, r)のうち残っているものの値段の和 とする。 xは降順なので1個ずつcntとsumを調整できる。 また、xを降順に見ていったとき、y,zは昇順であることに注意すると cnt,sumに対する更新はO(N)回で済む。 二分探索で cntに対するクエリがm-(x+y+z)となるようなクエリ[0, p)を満たすpを求めれば、 m-(x+y+z)個の価格の和をsumに対してクエリ[0, p)を投げて求められる。 実行時間 O(n(log(n))^2) */ int main(){ ios::sync_with_stdio(false); cin.tie(0); int N, M, K; cin >> N >> M >> K; vector<pair<ll,int> > C(N); vi A(N), id(N); rep(i, N) { cin >> C[i].first; C[i].second = i; } // 値段は安い方を優先して使いたいので昇順ソート sort(all(C)); vll cf(N); // ソート後のコスト、インデックス rep(i, N)cf[i] = C[i].first; rep(i, N)id[C[i].second] = i; for (int a : {1, 2}) { int t, x; cin >> t; while (t--) { cin >> x; --x; A[id[x]] |= a; } } vi X, Y, Z, DUMMY; rep(i, N) (A[i] == 3 ? X : A[i] == 2 ? Y : A[i] == 1 ? Z : DUMMY).push_back(i); // 集合X, Y, Zからいくつ選んだもののコストの和 ll cur = 0; each(x, X)cur += cf[x]; ll ans = LLONG_MAX; BIT cnt(N), sum(N); // Xに含まれないものをBITに加える rep(i, N)if (A[i] != 3) { cnt.add(i, 1); sum.add(i, cf[i]); } // 二分探索判定用 int need = -1; auto f = [&](int m) { return cnt.sum(m) >= need; }; auto g = [&](vi &W, int w, int a) { cur += a*cf[W[w]]; cnt.add(W[w], -a); sum.add(W[w], -a*cf[W[w]]); }; int y = 0, z = 0; for (int x = sz(X); x >= 0; --x) { // Xからx個選ぶ // YからK-x個以上選ばなければならない。 while (x + y < K && y<sz(Y)) g(Y, y++, +1); // ZからK-x個以上選ばなければならない。 while (x + z < K && z < sz(Z)) g(Z, z++, +1); // MashaかArkadyは不満足 if (x + y < K || x + z < K)break; // x+y+z>Mとすると多すぎて駄目 if (x + y + z <= M) { // あとM-x-y-z個必要 need = M - x - y - z; if (need == 0)smin(ans, cur); else { int w = binarySearchR(0, N, f); smin(ans, cur + sum.sum(w)); } } if (x) g(X, x - 1, -1); } cout << (ans != LLONG_MAX ? ans : -1) << endl; }
Codeforces #413 C: Fountains
解説付きコード
/* 解候補は4種類ある。 何も買わない コインとダイヤモンドでそれぞれ1個ずつ噴水を買う コインで2個噴水を買う ダイヤモンドで2個噴水を買う 前二者は自明 後二者について 噴水をコインで2個買うとする 安い方の必要なコイン数を固定すると、 使える残りのコイン数が決まる。 そのコインの数以下で変える最大の美しさを持つ噴水も確定する。 よって、安い方の噴水を昇順で固定して、 それより安い噴水と高くて買えない噴水を候補から外す。 */ /* コインだけ、もしくはダイヤモンドだけで2個の噴水を買いたい */ int f(vector<pii> &a, int m) { // price_beauty, beauty_price // 前者は値段で、後者は美しさで // 最大値、最小値を取得できる multiset<pii> p_b, b_p; auto g = [&](int p, int b) { // multisetの削除はイテレータを使うこと // そうでないと重複要素をすべて削除してしまう。 p_b.erase(p_b.find(mp(p, b))); b_p.erase(b_p.find(mp(b, p))); }; rep(i, sz(a)) { p_b.insert(a[i]); b_p.insert(mp(a[i].second,a[i].first)); } int res = 0; while (sz(p_b) > 1) { int p1, b1; // 安い方の噴水の値段,美しさ tie(p1, b1) = *p_b.begin(); if (p1 > m)break; // この噴水を解候補から削除 g(p1, b1); // あとlimコインだけ使える int lim = m - p1; // 高すぎる噴水を削除 while (sz(p_b) && p_b.rbegin()->first > lim) { int p, b; tie(p, b) = *p_b.rbegin(); g(p, b); } if (sz(p_b) == 0)break; // 買える噴水のうち最も美しいもの int b2 = b_p.rbegin()->first; smax(res, b1 + b2); } return res; } int main(){ ios::sync_with_stdio(false); cin.tie(0); int N, C, D; cin >> N >> C >> D; vector<pii> cs, ds; int mac = 0, mad = 0; rep(i, N) { int b, p; char c; cin >> b >> p >> c; if (c == 'C') { cs.emplace_back(p, b); if (p <= C) { // ここをmac=bとしてしまった smax(mac, b); } } if (c == 'D') { ds.emplace_back(p, b); if (p <= D) { // ここをmad=bとしてしまった smax(mad, b); } } } int ans = 0; // 何も買わない場合がある if (mac > 0 && mad > 0)ans = mac + mad; // コインとダイヤモンドを両方使う場合 // コインだけ、もしくはダイヤモンドだけ smax(ans, max(f(cs, C), f(ds, D))); cout << ans << endl; }
Codeforces #413 D: Field expansion
まずa[i]は大きい方を優先して使ったほうがいいので降順にソートしておく。
2^17>10^5かつa[i]>=2より
掛け算は縦横合わせてたかだか17+17=34回
よって
f[i番目までは掛けた][横の長さ]=縦の長さの最大値
をDPで解けばいい。
AOJ 2606 : Perm Query
順列はいくつかのサイクルで表記できる。
[l, r)に含まれるサイクルの長さをc[l],...,c[r-1]のように表すと
lcm(c[l], ..., c[r])回だけ、各要素は値が変わる。i番目の要素は
lcm/c[i] 回だけサイクルを回るので、そのサイクルに含まれる数の和をS[i]とすると
i番目の要素についての和は
S[i]*lcm/c[i]
l≦i<rで和を取って
Σ[l≦i<r](S[i]*lcm/c[i])
がクエリ[l, r)に対する解。
問題はlcmの求め方で、lcmは大きい数になりうるのでmod 10^9+7で計算したい。
つまり
[l, r)に含まれるすべてのサイクルの長さについてlcmを計算したい。
[l, r)はO(N)の長さがあって1要素ずつ見ていくと間に合いそうにない。
そこでサイクルの長さごとに見ていく。
サイクルの長さの種類はたかだかO(√N)個しかない。なぜなら、サイクルの長さの和はNなので、
サイクルの長さの種類が最大となるのは
1+2+...+(k-1)+k = N
のような場合であるため。
よって、O(√N)個のすべてのサイクルの長さについて、そのサイクルの出現数を部分和で持っておけば、
各サイクルの長さが[l, r)で出現するかどうかすぐわかる。
事前にサイクルの長さに対して素因数分解しておけば、素因数の数はたかだかO(log(N))個なので
各クエリに対してO(log(N)√N)
全体でO(Qlog(N)√N)
int main(){ ios::sync_with_stdio(false); cin.tie(0); int N, Q; cin >> N >> Q; vi p(N), vis(N); // S[i]/c[i]の部分和 vector<mint> sm(N + 1); // 素因数分解の結果 unordered_map<int, map<int, int> > fa; // lns[i]は長さiのサイクルの出現の部分和 unordered_map<int, vi> lns; rep(i, N)cin >> p[i], p[i]--; rep(i, N)if (!vis[i]) { // 新しいサイクルを見つけた vi a; ll s = 0; int x = i; do { a.push_back(x); vis[x] = 1; // サイクルに含まれる数の和 s += x + 1; x = p[x]; } while (x != i); int len = sz(a); if (!fa.count(len)) { fa[len] = factorize(len); lns[len] = vi(N + 1); } each(y, a) { // S[i]/c[i] sm[y + 1] = mint(s) / len; // 長さlenのサイクルはy番目を含む lns[len][y + 1] = 1; } } // 部分和の計算 rep(i, N)sm[i + 1] += sm[i]; each(q, lns) { vi &v = q.second; // 出現数の部分和 rep(i, N)v[i + 1] += v[i]; } while (Q--) { int l, r; cin >> l >> r; --l; mint s = sm[r] - sm[l], lcm = 1; // 各素因数について、素因数分解したときに最も多く現れたときの指数 unordered_map<int, int> ma; each(q, lns) { int len = q.first; vi &v = q.second; if (v[r] - v[l]) { each(ii, fa[len]) { // ここが最も時間がかかる smax(ma[ii.first], ii.second); } } } // 素因数分解→lcm each(q, ma) while (q.second--)lcm *= q.first; // s=Σ(S[i]/c[i]) cout << s*lcm << endl; } }